2005 год. В рамках 12-го тура испанской Примеры "Барселона" на "Сантьяго Бернабеу" крупно переигрывает мадридский "Реал" - 0:3. Этот матч называют бенефисом Роналдинью, которому рукоплескал стадион извечного соперника. Бразилец забил в этой игре два гола, в обоих случаях красиво пройдя половину поля, попутно обыграв нескольких игроков "Реала".
|
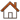
|
|
|||||||
| Тотализатор | Вопросы | Регистрация | Справка | Пользователи | Календарь | Поиск | Сообщения за день | Все разделы прочитаны |
|
|
Опции темы | Поиск в этой теме | Опции просмотра |
|
|
Цитата выделенного #11 | |||||
Регистрация: 08.05.2008 Сообщения: 1,859 Сказал(а) спасибо: 783 Поблагодарили: 2,476 раз(а) в 1,245 сообщениях
Деньги: 11500$
Место в рейтинге: 26
|
Тут скорее не "Решение ваших проблем", а "Решение ваших интересов".
Делать нечего, решил попробовать решать задачи по теории вероятностей, которая предстоит скоро. Так вот, условие задачи: случайная величина X имеет нормальный закон распределения с параметрами a и σ^2 (дисперсия). Найти параметр a, если известно, что σ (среднеквадр.отклонение) = 1,2 и P (X > 3) = 0,5. Вычислить вероятность того, что значение случайной величины X окажется больше 5. У кого-нибудь есть мысли?  Наверно, если бы проходил, то знал бы решение этой, наверняка, элементарщины, а так интересно узнать. |
|||||
| Offline |

|











 Древовидный вид
Древовидный вид